고체물리학
저번 글에서 고체의 비열을 설명하기 위한 볼츠만(Boltzmann)의 접근 방법에 대해서 알아보았어요.
이번에는 아인슈타인(Einstein)의 접근 방법에 대해서 알아보도록 해요!
어떤 고체의 내부에는 아주 많은 원자가 들어 있겠죠.
그래서 아인슈타인은 통계역학적 방법을 통해 이 문제에 접근하였어요.
일단, 모든 원자가 동일한 진동수 ω의 퍼텐셜에 놓여 있다고 보는 것이에요.
그렇다는 것은, 원자들이 이렇게 배열되어 있다는 이야기가 되어요.

모든 원자들이 같은 진동수를 가지는 조화진동자라는 것이죠!
이는 볼츠만의 설명과도 같아요.
실제로는 저번에 설명한 바와 같이, 모두 3차원 조화진동자로 가정해야 할 것이지만,
먼저 1차원 조화진동자를 어떻게 계산하는지 알면 3차원은 쉽게 일반화 할 수 있겠죠.
1차원 조화진동자의 에너지 고유값은 다음의 식으로 표현할 수 있어요.

그리고 원자는 아주 많으니까 이러한 조화진동자도 똑같은 수 만큼 아주 많을 것이죠.
그렇다면 이러한 조화진동자들의 에너지를 전부 합치게 되면, 고체가 가지고 있는 에너지의 양을 알 수 있을 거에요.
그것을 알아내기 위해, 통계역학적 방법을 써 볼게요.
어떤 고체에 속하는 각각의 조화진동자들은 서로 다른 에너지를 가지고 있을 것이에요.
누군가는 조금 더 많은 에너지를 가지고 있을 수도 있고, 누군가는 조금 더 적은 에너지를 가지고 있을 수도 있죠.
그러나, 각각의 조화진동자가 가지는 에너지는 특정 값만이 가능해요.
위 식에서, 각각의 n마다 고유한 에너지 상태 Eₙ이 정해진다는 것을 알 수 있어요.
만약 n이 정수라면 어떨까요? Eₙ은 특정한 값 만을 가질 수 있으며, 불연속적으로 분포할 것이라는 사실을 알 수 있겠죠?
이러한 n을 이 진동자의 양자수라고 하고, 0 이상의 정수만이 가능해요.
그렇다면, 고체 전체에서 E₁의 에너지 상태를 가지는 조화진동자의 수와 E₂의 에너지 상태를 가지는 조화진동자의 수는 같을까요?
E₃ , E₄ , E₅ ... Eₖ 는 어떤가요? 모두 동일한 비율로 존재할까요?
그렇지 않겠죠?
만약 그렇다면, k가 무한에 가까운 수라고 할 때, 고체 전체의 에너지는 무한에 가까운 수가 될 테니까요.
고체 전체에서, 각각의 에너지 상태 E₁ , E₂ , E₃ ... Eₙ 이 가지는 확률 비중은

으로 구할 수 있어요. Eₙ이 증가함에 따라 값이 작아지는 형태에요.
높은 에너지 상태일수록 존재할 확률이 적어진다는 것이죠.
이는 낮은 에너지일 수록 안정하다는 일반적인 상식과도 부합하여요.
이것을 우리는 볼츠만 가중치라고 불러요.
이전 글에 나오셨던 볼츠만 이 맞아요! 통계역학의 시초이셔서 자주 등장하시죠.
이러한 볼츠만 가중치를 통해 각 에너지 상태가 존재할 확률을 구할 수 있어요.
특정 사건이 일어날 확률은 특정 사건이 일어나는 경우의 수를 전체 경우의 수로 나누어 구할 수 있었죠?
마찬가지로, 각각의 조화진동자가 특정 에너지 상태를 가질 확률은
특정 에너지 상태의 확률 비중을 모든 에너지 상태의 확률 비중의 합으로 나누어서 구할 수 있어요.

여기서 우변의 분모에 주목해주세요.
분모가 전체 에너지 상태의 확률의 합을 1로 만들어주는 역할을 하고 있죠?
이를 정규화라고 해요.
그리고 정규화를 해 주는 이 식을 '분배함수(partition function)' 라고 불러요.

분배함수를 이용하면 고체의 내부에너지(모든 조화진동자들의 에너지의 합)을 구할 수 있어요.
어떻게 구할 수 있을까요?
모든 조화진동자들이 가진 에너지의 합을 구하기 위해서는,
각 에너지 상태가 가진 에너지를 알아야겠죠? 이는 Eₙ으로 알 수 있어요.
그리고 이러한 에너지를 가진 조화진동자가 전체에서 얼마나 분포하는지도 알아야 할 것이에요. 이는 확률 pₙ으로 알 수 있어요.
그리고 이 둘을 곱하면 양자수 n에 해당하는 에너지가 얼마나 있는지 알 수 있겠죠?
이를 모든 n에 대해서 시행하여 모두 더하면 그것이 모든 조화진동자들이 가진 에너지의 합이라는 것이죠.

<E>는 간단하게 말하면 에너지의 평균값이라는 의미에요.
여기서는 '모든 조화진동자들의 평균 에너지 값' 이라고 생각하셔도 괜찮아요.
이 값은 분배함수를 통해 구할 수 있는데, 어떻게 분배함수 Z로 평균 에너지 <E>를 구할 수 있는지 알아볼게요.
먼저, <E>에 대한 식을 아래처럼 만들어볼게요.

그런데 이러한 형태는 분배함수에서 유도할 수 있어요.
분배함수 Z를 β로 편미분하면,

이러한 결과를 얻을 수 있어요.
위 식의 일부와 똑같이 생겼죠? 그러면..

이렇게 정리할 수 있어요. 따라서 분배함수 Z에 자연로그를 취한 뒤, 그 값을 β로 편미분하면
평균 에너지 <E>를 구할 수 있는 것이죠.
이제 1차원 조화진동자의 분배함수를 구하고, 이를 통해 고체의 평균 에너지를 구해보도록 할게요.

앞에서 언급한 1차원 조화진동자의 에너지 고유값 Eₙ의 식을 분배함수 Z에 넣어 얻은 결과에요.
이 식은 무한등비급수의 형태를 가지고 있어요.

이러한 무한등비급수의 합은 첫 번째 항 a와 공비 r을 통해 다음과 같은 공식으로 계산할 수 있어요.


여기서 쌍곡함수로 변환하면 더욱 간단한 형태를 얻을 수 있어요.


따라서 최종적으로 다음과 같은 결론을 얻게 되어요.

이제 분배함수 Z를 구했으니 평균 에너지 <E> 를 구해보도록 할게요.
일단 분배함수와 평균 에너지의 관계는 이렇다는 것을 알고 있죠.

이제 실제로 계산을 해 볼게요.
아무래도 문제가 되는 부분은 편미분 쪽이겠죠?

이러한 형태는 다음과 같이 계산할 수 있어요.

따라서 편미분을 계산하면,

이러한 식을 얻을 수 있어요.
이제 이 식을 이용해서 평균 에너지 <E>를 구하면

마지막으로 쌍곡함수를 다시 변환하면


이때, 보스 점유인자(Bose occupation factor) 라는 것이 있어요.

이를 이용해서 다시 한번 변환해주면 최종적으로 다음 식을 얻어요.

이렇게 얻어진 식의 물리적인 의미를 알아보도록 할게요.

이 글의 위에서 이러한 식을 보신 적이 있으실 거에요.
1차원 조화진동자의 에너지 고유값이에요.
방금 구해진 평균 에너지 <E> 와 비슷하죠?
그러니까 이 식은, n_B에 해당하는 조화진동자 하나의 에너지 값이라고 할 수 있는 거에요.
이러한 조화진동자가 고체 내부엔 원자 수 만큼 있는 것이죠.
우리는 조화진동자들의 평균 에너지 를 구했기 때문에,
모든 조화진동자의 에너지가 <E> 에 해당한다고 생각할 수 있어요.
이제 조화진동자들의 평균 에너지 <E>를 이용해 비열 C를 구해보도록 할게요.
비열은 '어떤 물질의 온도를 1도 올리는 데 필요한 에너지의 양' 이였죠?
그래서 에너지를 온도에 대해서 미분하면 비열을 구할 수 있어요.

이 식을 계산해보도록 할게요.
먼저, 우리가 구한 조화진동자당 평균 에너지 <E> 에는 T가 없죠.
하지만 이미 들어있어요.
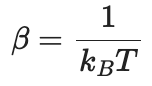
β는 사실 T에 대한 식이였어요.

따라서 위와 같이 변환할 수 있는 것이죠. 이를 통해 <E>를 T에 대해서 미분해보죠.

상수 부분인 1/2는 미분 과정에서 어차피 제거될 것이므로 다음이 성립하고,
합성함수 미분에서의 연쇄 법칙(Chain rule)에 의해


비열 C에 대해서 다음 식을 얻을 수 있어요.
하지만 저번 글에서 보셨다시피, 원자는 x, y, z 의 3개 축으로 진동할 수 있었죠?
그래서 원자 1개당 조화진동자 3개가 있는 셈이에요.
그러니까 고체에서의 비열은 위에서 구한 값의 3배에요.
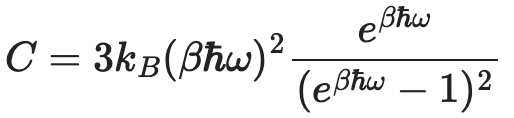
따라서 최종적으로 비열은 다음 식으로 구할 수 있게 되어요.
하지만 이 식은 뒬롱-프티(Dulong-Petit) 법칙인 $C=3R$ 이랑은 비슷하면서도 다르게 생겼죠.
이 식은 고온에서 $C=3k_B$ 에 도달하게 되어요.
$\beta=\frac{1}{k_B T}$임을 감안하면, T->$infty$에서 $\beta \hbar \omega$->0 이 됨을 알 수 있어요.
계산을 용이하게 하기 위해 $\beta \hbar \omega=x$라 할게요.
x가 0에 근접할 때, $e^x$는 테일러 전개를 통해 다음과 같이 근사할 수 있어요.
$$e^x\approx 1+x+\frac{e^x}{(e^x-1)^2}\approx 1+x$$
x가 매우 작기 때문에 2차 이상의 고차항 영향은 무시할 수 있다고 근사한 것이에요.
이제 이를 바탕으로 식을 다시 정리하면
$$C=3k_Bx^2\frac{1+x}{x^2}$$
분모와 분자의 $x^2$를 서로 약분하고, x->0을 대입하면
$$C=3k_B$$
고온에서의 뒬롱-프티 법칙 식이 나오는 것이죠!
R 대신 $k_B$가 등장한 이유는, 위 계산이 단일 원자에 한정해서 이루어진 것이기 때문이에요.
그렇다면 이 식은 어떻게 다이아몬드의 비열을 설명할 수 있었을까요?
아인슈타인 진동수 ω는 다음의 식으로 구할 수 있어요.

여기서 k는 스프링 상수(Spring constant)에요.
스프링의 길이 변화를 위해 얼마만큼의 힘을 가해야 하는지에 대한 비율이죠.
이 값이 높은 스프링은, 늘리거나 줄이려면 더 많은 힘이 필요해요.
우리는 원자 간 결합을 스프링으로 생각했기 때문에,
이 값이 높다는 것은 원자간 결합의 세기가 강하다는 것을 의미해요.
그리고 m은 원자 질량(mass)이에요.
다이아몬드의 경우, 상대적으로 가벼운 원자(탄소 C, 원자량 12)들로 구성되어 있지만,
매우 단단한 결합을 가지고 있어요.
그래서 ω 의 크기가 큰 것이죠.
대부분의 물질들에서 ω는 상온(약 300K)과 비교하면 충분히 작지만,
다이아몬드의 ω는 더 크기 때문에, C=3R이라는 Dulong-Petit 법칙과 거리가 멀었던 것이에요.
그래서 고온에서는 다이아몬드도 C=3R에 가까워져요.
그러나 이러한 아인슈타인의 계산에서도 문제가 발견되었어요.
고온에서의 비열과 다이아몬드 등의 여러 물질들이 C=3R을 만족하지 않는 이유를 잘 설명했지만,
저온에서는 실제 실험값과 분명한 편차가 존재했기 때문이에요.
대부분의 물질은 저온에서의 비열 C가 온도 T³에 비례하는데,
아인슈타인의 계산은 이를 설명하지 못했던 것이죠.
그래서 이를 잘 설명할 수 있는 방법을 디바이(Debye)가 알아내게 되었어요.
디바이의 방법에 대해서 다음 글에서 알아보도록 할게요.
이 글은 제가 스스로 공부하며 이해한 내용을 정리하기 위해 쓰여졌어요.
만약 이 글의 내용에 오류가 있다면, 저와 다른 사람을 위해 댓글로 지식을 나누어주세요!
'학습 > 고체물리학' 카테고리의 다른 글
| [고체물리학] 금속 내부의 전자-드루드 이론 (0) | 2025.11.20 |
|---|---|
| [고체물리학] 비열-디바이의 이론 (0) | 2025.09.18 |
| [고체물리학] 비열-볼츠만의 이론 (0) | 2025.09.11 |